Curiosamente los resultados ponen de manifiesto los aspectos de la propiedad del tiempo, o por simplificar, la fractalidad de éste. El análisis de las líneas temporales, muestra una lógica universal que puede ser analizada desde patrones individuales o conjuntos.
Destacamos la calidad de la argumentación científica, presentada por Monika Bartkowiak, Adam Miranowicz, Xiaoguang Wang, Yu-xi Liu, Wieslaw Leonski, Franco Nori, que no ha estado exenta de polémica en el marco de los planteamientos más ortodoxos de la comunidad científica.
Cabe destacar la valentía argumental y la elegancia del modelo propuesto, que enlaza sistemáticamente con las premisas del Global Scaling que ya fueron formuladas en su día por Müller.
Reproducimos textualmente el Abstract del estudio:
Recently, analyses of phenomena exhibiting finite-time decay of quantum entanglement have attracted much attention. Such decay is often referred to as sudden vanishing (sudden death) of entanglement, which can be followed by its sudden reappearance (sudden rebirth). We analyze various finite-time decays (for dissipative systems) and analogous periodic vanishings (for unitary systems) of nonclassical correlations as described by violations of classical inequalities and the corresponding nonclassicality witnesses (or quantumness witnesses), which are not necessarily entanglement witnesses. We show that these sudden vanishings are universal phenomena and can be observed: (i) not only for two- or multi-mode but also for single-mode nonclassical fields, (ii) not solely for dissipative systems, and (iii) at evolution times which are usually different from those of sudden vanishings and reappearances of quantum entanglement.Definen la ecuación envolvente del tiempo como un estado basado en Werner (Un fractal) el el que la onda predomina sobre la partícula :
y de forma detallada, despejan cada línea temporal:
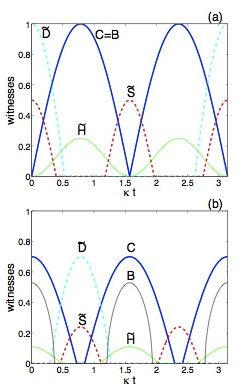
Por tanto, la representación aislada del tiempo lineal quedaría así:
Donde de forma consolidada tendríamos las diferentes líneas de tiempo:
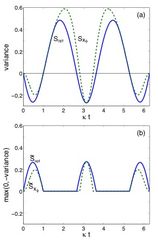
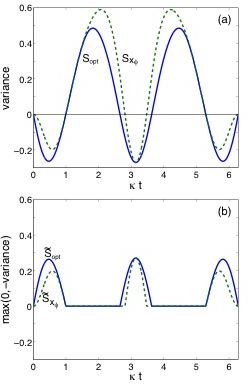
En la página 6 del Paper, señalan expresamente, que para realizar la conversión y el análisis temporal es necesario comparar el tiempo con la frecuencia, y que ambas dos variables son dependientes entre sí, lo que aproxima bastante a una formulación de la lógica de los osciladores armónicos en el modelo.
Respecto a la lógica de los parámetros de conversión, parten de un estado inicial que evoluciona a partir de la siguiente equivalencia en el operador PHI relativo al tiempo :
Pueden acceder al estudio completo aquí
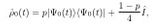
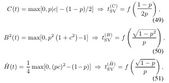
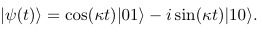



Comentarios del Lector
a nuestro Boletín